Toán hình 9 - Ôn Thi Vào Lớp 10 - Bài 16-->26
Bài 17 Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax và dây AC bất kỳ. Tia phân giác của góc xAC cắt nửa đường tròn tại D, các tia AD và BC cắt nhau tại E.
a) Chứng minh DABE cân.
b) Đường thẳng BD cắt AC tại K, cắt tia Ax tại F . Chứng minh tứ giác ABEF nội tiếp.
Bài 18 Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB; AC và cát tuyến AMN không đi qua tâm O. Gọi I là trung điểm MN.
a) Chứng minh AB2 = AM. AN
b) Chứng minh tứ giác ABIO nội tiếp .
c) Gọi D là giao điểm của BC và AI. Chứng minh 
Bài 19 Cho tam giác ABC nội tiếp đường tròn (O). Phân giác trong của 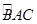 cắt BC tại D và cắt đường tròn tại M. Phân giác ngoài tại Acắt đường thẳng BC tại E và cắt đường tròn tại N. Gọi K là trung điểm của DE. Chứng minh:
cắt BC tại D và cắt đường tròn tại M. Phân giác ngoài tại Acắt đường thẳng BC tại E và cắt đường tròn tại N. Gọi K là trung điểm của DE. Chứng minh:
a) MN vuông góc với BC tại trung điểm của BC.
c) AK là tiếp tuyến của đường tròn (O).
Bài 20 Cho ba điểm A, B,C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C. Từ A vẽ hai tiếp tuyến AM và AN . Gọi E và F lần lượt là trung điểm của BC và MN.
a) Chứng minh AM2 = AN2 = AB. AC
b) Đường thẳng ME cắt đường tròn (O) tại I. Chứng minh IN // AB
c) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác OEF nằm trên một đường thẳng cố định khi đường tròn (O) thay đổi.
Bài 21 Cho đường tròn (O) đường kính AB = 2R . Điểm C nằm trên (O) mà AC > BC. Kẻ CD ^ AB ( D Î AB ) . Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Tiếp tuyến tại C của đường tròn (O) cắt AE tại M. OM cắt AC tại I . MB cắt CD tại K.
a) Chứng minh M là trung điểm AE.
b) Chứng minh IK // AB.
c) Cho OM = AB. Tính diện tích tam giác MIK theo R.
Bài 22 Trên cung nhỏ BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Gọi là giao điểm của AP và BC.
a) Chứng minh BC2 = AP . AQ .
b) Trên AP lấy điểm M sao cho PM = PB . Chứng minh BP+PC= AP.
Bài 23 Cho nửa đường tròn (O) đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn. CA cắt nửa đường tròn ở M, CB cắt nửa đường tròn ở N. Gọi H là giao điểm của AN và BM.
a) Chứng minh CH ^ AB .
b) Gọi I là trung điểm của CH. Chứng minh MI là tiếp tuyến của nửa đường tròn (O).
c) Giả sử CH =2R . Tính số đo cung  .
.
Bài 24 Cho nửa đường tròn đường kính AB = 2R và dây MN có độ dài bằng bán kính (M thuộc cung AN). Các tia AM và BN cắt nhau ở I. Các dây AN và BM cắt nhau ở K.
b) Tìm quỹ tích điểm I và quỹ tích điểm K khi dây MN thay đổi vị trí .
c) Chứng minh I là trực tâm của tam giác KAB .
d) AB và IK cắt nhau tại H . Chứng minh HA.HB = HI.HK .
e) Với vị trí nào của dây MN thì tam giác IAB có diện tích lớn nhất? Tính giá trị diện tích lớn nhất đó theo R.
Bài 25 Trên đường tròn (O) lấy ba điểm A, B và C. Gọi M, N và P theo thứ tự là điểm chính giữa của các cung AB, BC và AC. BP cắt AN tại I, NM cắt AB tại E.
Gọi D là giao điểm của AN và BC. Chứng minh rằng:
a) DBNI cân. b) AE.BN = EB.AN. c) EI // BC. d)  .
.
Bài 26 Cho hai đường tròn (O) và (O1) ở ngoài nhau. Đường nối tâm OO1 cắt các đường tròn (O) và (O1) tại các điểm A, B, C, D theo thứ tự trên đường thẳng. Kẻ tiếp tuyến tuyến chung ngoài EF (E Î (O), F Î (O1)). Gọi M là giao điểm của AE và DF, N là giao điểm của EB và FC. Chứng minh rằng:
a) Tứ giác MENF là hình chữ nhật.
b) MN ^ AD.
c) ME . MA = MF . MD.
--- HẾT----
Tags: Các bài Toán Hình Ôn Thi Vào Lớp 10






 Trang Trước
Trang Trước







không có lời giải ạ? :((
ReplyDeleteko có giải ạ???
ReplyDelete