CHUYÊN ĐỀ PHƯƠNG TRÌNH
CHUYÊN ĐỀ PHƯƠNG TRÌNH
I.PHƯƠNG PHÁP THƯỜNG VẬN DỤNG:
1. Đưa về phương trình tích
a) Các bước
![]() Tìm tập xác định của phương trình.
Tìm tập xác định của phương trình.
![]() Dùng các phép biến đổi đại số, đưa phương trình dạng f(x) . g(x) … h(x) = 0 (gọi là phương trình tích). Từ đó suy ra f(x) = 0; g(x) = 0; … ; h(x) = , là những phương trình quen thuộc. Nghiệm của phương trình là tập hợp các nghiệm của các phương trình f(x)=0; g(x) = 0; … ;h(x) = 0 thuộc tập xác định.
Dùng các phép biến đổi đại số, đưa phương trình dạng f(x) . g(x) … h(x) = 0 (gọi là phương trình tích). Từ đó suy ra f(x) = 0; g(x) = 0; … ; h(x) = , là những phương trình quen thuộc. Nghiệm của phương trình là tập hợp các nghiệm của các phương trình f(x)=0; g(x) = 0; … ;h(x) = 0 thuộc tập xác định.
![]() Đôi khi dùng ẩn phụ thay thế cho một biểu thức chứa ẩn, đưa về dạng tích (với ẩn phụ). Giải phương trình với ẩn phụ, từ đó tìm nghiệm của phương trình đã cho.
Đôi khi dùng ẩn phụ thay thế cho một biểu thức chứa ẩn, đưa về dạng tích (với ẩn phụ). Giải phương trình với ẩn phụ, từ đó tìm nghiệm của phương trình đã cho.
![]() Dùng cách nhóm số hạng, hoặc tách các số hạng … để đưa phương trình về dạng quen thuộc mà ta đã biết cách giải
Dùng cách nhóm số hạng, hoặc tách các số hạng … để đưa phương trình về dạng quen thuộc mà ta đã biết cách giải
b) Thí dụ
1.Giải phương trình:
Giải
Bài tập áp dụng:
2.Giải phương trình:
Giải
Gợi ý: Áp dụng hằng đẳng thức: (a-b)3 + (b-c)3 + (c-a)3 = 3(a-b)(b-c)(c-a)
3.Giải phương trình:
Đs: 2
4. Giải phương trình:
Đs: -13; 2
5. Giải phương trình:
Đs: 1994
6. Giải phương trình:
Đs:1
7. Giải phương trình:
8. Giải phương trình:
(câu 3 dề 52 bộ tuyển sinh đại học 1993)
Đs: 2 ; -2
9. Giải phương trình:
(Trích câu 2 đề 78 bộ dề thi tuyển sinh đại học 1993)
2. Áp dụng bất đẳng thức
a) Các bước
![]() Biến đổi phương trình về dạng f(x) = g(x) mà f(x) ≥ a; g(x) ≤ a (a là hằng số)
Biến đổi phương trình về dạng f(x) = g(x) mà f(x) ≥ a; g(x) ≤ a (a là hằng số)
Nghiệm của phương trình là các giá trị x thỏa mãn đồng thời f(x) = a và g(x) = a
![]() Biến đổi phương trình về dạng h(x) = m (m là hằng số)mà ta luôn có h(x) ≥ m hoặc h(x) ≤ m thì nghiệm của hệ là các giá trị x làm cho dấu đẳng thức xảy ra.
Biến đổi phương trình về dạng h(x) = m (m là hằng số)mà ta luôn có h(x) ≥ m hoặc h(x) ≤ m thì nghiệm của hệ là các giá trị x làm cho dấu đẳng thức xảy ra.
b) Thí dụ
1. Giải phương trình:
Giải
Áp dụng bất đẳng thức Bunhiacốpki cho 4 số:
Bài tập áp dụng:
2. Giải phương trình:
3. Giải phương trình:
Đs: phương trình vộ nghiệm
4. Giải phương trình:
Đs:x = 3
5. Giải phương trình:
Đs: 1
3. Chứng minh nghiệm duy nhất
a) Các bước
Ở một số phương trình ta có thể thử trực tiếp để thấy nghiệm của chúng, rồi tìm cách chứng minh rằng ngoài nghiệm này ra không còn nghiệm nào khác nữa.
b) Thí dụ
1. Giải phương trình:
Giải:
Do đó x ≠ 0 không thể là nghiệm của (1) Đs: 0
Bài tập áp dụng
2. Giải phương trình:
Đs: 2
3. Giải phương trình:
4. Giải phương trình:
Đs: 2
5. Giải phương trình:
Đs: 3 ; 4
6. Giải phương trình:
Đs: ±2
4. Đưa về hệ phương trình
a) Các bước
![]() Tìm điều kiện tồn tại của phương trình
Tìm điều kiện tồn tại của phương trình
![]() Biến đổi phương trình để xuất hiện nhân tử chung
Biến đổi phương trình để xuất hiện nhân tử chung
![]() Đặt ẩn phụ thích hợp để đưa việc giải phương trình về việc giải hệ phương trình quen thuộc
Đặt ẩn phụ thích hợp để đưa việc giải phương trình về việc giải hệ phương trình quen thuộc
b) Thí dụ
1. Giải phương trình:
Giải:
u, -v là nghiệm của phương trình ![]()
![]() Nếu
Nếu ![]() thì
thì ![]() : phương trình vô nghiệm
: phương trình vô nghiệm
Bài tập áp dụng:
2. Giải phương trình:
Đs: 0
3. Giải phương trình
















 Trang Trước
Trang Trước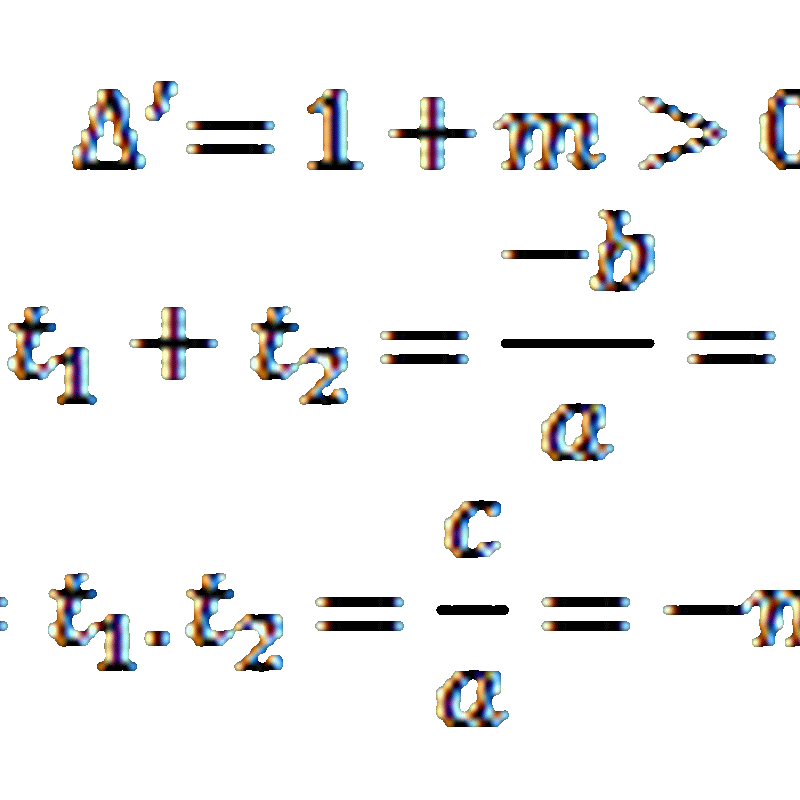







No comments: